EMC Question of the Week: August 7, 2023
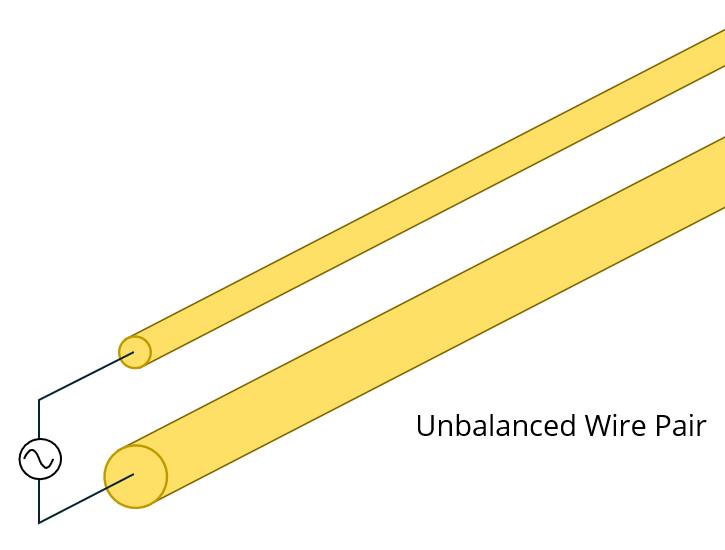
An isolated differential source drives an unbalanced wire pair. One wire in the pair has a 1-mm diameter and the other wire has a 2-mm diameter. If the source supplies 10 mA of current, what is the common-mode current on the wire pair?
- zero
- between 1 mA and 9 mA
- 10 mA
- more than 10 mA
Answer
The best answer is “a.” The source draws current from one wire and puts the same amount of current on the other wire. The current on wire 1, I1, is the negative of the current on wire 2, I2. The common mode current is the sum of the current on both wires, (i.e., I1 + I2 = I1 + -I1 = 0).
The expression for the differential-mode current on an unbalanced line is IDM = (1-h) I1 - (h) I2, where h is the imbalance factor. No matter what the value of h is, if I1 = -I2, the magnitude of the differential-mode current is, |IDM| = |I1| = |I2|. In this case, the differential-mode current is 10 mA.
Without any calculations at all, this question could be answered by recognizing that imbalance does not cause mode conversion. Mode conversion can only occur when there is a change in the imbalance.
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
