EMC Question of the Week: December 9, 2024
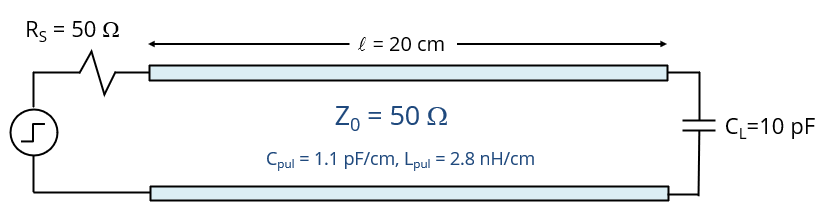
A 50-Ω source drives a 10-pF load capacitance through a 20-cm circuit board trace. The controlled-impedance trace has a 50-Ω characteristic impedance and a per-unit-length capacitance of 1.1 pF/cm. If the source voltage is an ideal step function, what is the rise-time observed at the load?
- << 1 ns
- 1 ns
- 2 ns
- 3.5 ns
Answer
The best answer is “b.” The 50-Ω voltage source charges the 10-pF capacitance with a rise-time equal to 2.2RC, which (in this case) is approximately 1 ns. Note that the initial waveform propagating from the source towards the load has a very fast transition time and is half the amplitude of the source open-circuit voltage. When this wavefront reaches the load, the voltage drops to zero and then climbs to the open circuit amplitude in about 1 ns.
This transmission line is matched at the source end, but not at the load end. This is generally the preferred method for matching a transmission line when the signal propagates in one direction from a single source to a single receiver. In this example, the propagation delay is approximately 1 ns. The transition time is less than twice the propagation delay, so a matched termination is definitely required.
If the 1 ns transition time were not necessary, slowing the transition time would generally be a much better option than matching the transmission line. For example, if the data rate was 10 Mbps or slower, the transition time could be increased to 10 ns by adding a resistor in series with the source. Since 10 ns is much greater than twice the propagation delay, a matched termination would not be necessary or desirable.
To get a 10-ns transition time, we use the same formula (2.2RC), however in this case the value of C includes both the load capacitance and the trace capacitance. For this example, C would be 32 pF (1.1 x 20 + 10) so the required value of R would be 142 Ω (or 92 Ω in series with the 50-Ω source).
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
