EMC Question of the Week: January 22, 2024

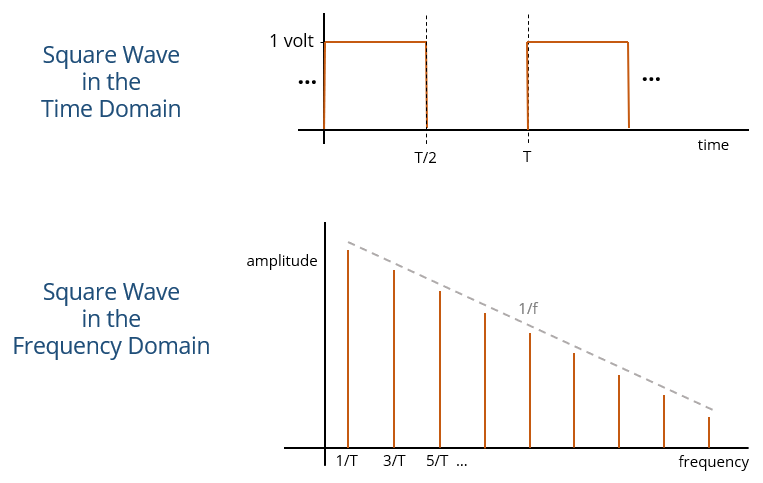
If a 200-MHz square wave with a peak-to-peak amplitude of 1.0 volt is input to a spectrum analyzer, the measured amplitude of the first harmonic should be

1. 1.0 volt (120 dBμV)
2. 0.71 volts (117 dBμV)
3. 0.63 volts (116 dBμV)
4. 0.45 volts (113 dBμV)

Answer

The correct answer is “d.” From the one-sided Fourier series representation, the peak amplitude of the first harmonic of a square wave is 2/π times the peak-to-peak amplitude of the time domain waveform. A spectrum analyzer (or EMI test receiver) measures the rms amplitude of the harmonic, which is 1/√2 times the peak amplitude. So, the first harmonic has an amplitude that is 2/(π√2) = 0.45 times the peak-to-peak amplitude of the square wave. The third harmonic is one-third the amplitude of the first harmonic. The fifth harmonic is one-fifth the amplitude of the first harmonic. 

With this knowledge, it is straightforward to calculate the amplitude of any harmonic. To get the amplitude of the nth harmonic, multiply the peak-to-peak amplitude of the square wave by 0.45 and divide by n. Or, if you only need 1 significant figure of accuracy, simply divide the peak-to-peak amplitude by 2n.

If your waveform has a non-negligible transition time, t_r, then the upper harmonics are further reduced by a factor of f/f_c, where f_c = 1/(πt_r). So, for example, to quickly estimate the amplitude of the 25th harmonic of a 3.3-volt, 40 MHz clock signal that has a very fast transition time, the calculation is simply, 3.3/(2*25) ≈ 60 mV. However, with a 3 nsec transition time (f_c = 1/(3x10^-9π) ≈ 100 MHz, the amplitude of the same harmonic (1 GHz) is reduced by (1000/100). In other words, with a controlled transition time, the harmonic at 1 GHz is about 6 mV instead of 60 mV (20 dB lower).

Have a comment or question regarding this solution? We'd like to hear from you. Email us at This email address is being protected from spambots. You need JavaScript enabled to view it..