EMC Question of the Week: March 13, 2023

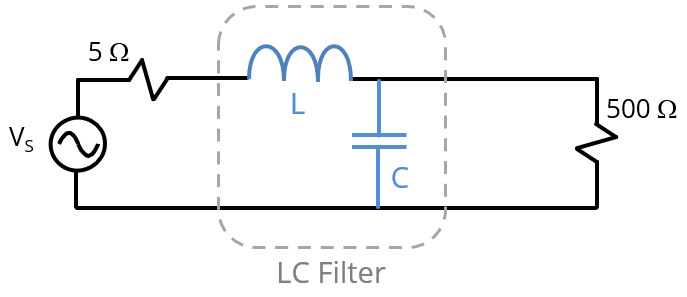
An LC low-pass filter is designed to attenuate noise from a 5-Ω source before it reaches a 500-Ω load. In order to avoid a resonance (negative insertion loss) near the cut-off frequency, the values of L and C should be chosen such that 

1. $\sqrt{\raisebox{1ex}{$\text{L}$}\!\left/ \!\raisebox{-1ex}{$\text{C}$}\right.}\text{ < 5 Ω}$
2. $\sqrt{\raisebox{1ex}{$\text{L}$}\!\left/ \!\raisebox{-1ex}{$\text{C}$}\right.}\text{ > 500 Ω}$
3. $\text{5 Ω < }\sqrt{\raisebox{1ex}{$\text{L}$}\!\left/ \!\raisebox{-1ex}{$\text{C}$}\right.}\text{ < 500 Ω}$
4. either (a.) or (b.)

Answer

The best answer is “d.” If we refer to $\sqrt{\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$C$}\right.}$ as the filter impedance, Z_filter, then the filter is matched to the source when Z_filter = 5 Ω. It is matched to the load when  Z_filter = 500 Ω. The cut-off frequency is $f_c=\frac{1}{2\pi \sqrt{LC}}$. When the filter is matched to the source or the load, the insertion loss is nearly 0 dB below the cut-off frequency and begins increasing at 40 dB/decade above the cut-off frequency. There is a slight negative insertion loss near cut-off.

When Z_filter < 5 Ω, the filter is overdamped. For Z_filter << 5 Ω, the inductor doesn't contribute, and the insertion loss is the same as that of a first-order RC filter. When Z_filter > 500 Ω, the filter is also overdamped. For Z_filter >> 500 Ω, the capacitor doesn't contribute, and the insertion loss is the same as that of a first-order RL filter.

When 5 Ω < Z_filter < 500 Ω, the filter is underdamped. This creates a resonance near the cut-off frequency where the insertion loss goes negative. To maximize the effectiveness of an LC filter, without a significant spike in the insertion loss near cut-off, it is generally desirable to match the source or the load resistance (or perhaps be slightly overdamped). 

Have a comment or question regarding this solution? We'd like to hear from you. Email us at This email address is being protected from spambots. You need JavaScript enabled to view it..