EMC Question of the Week: January 9, 2023
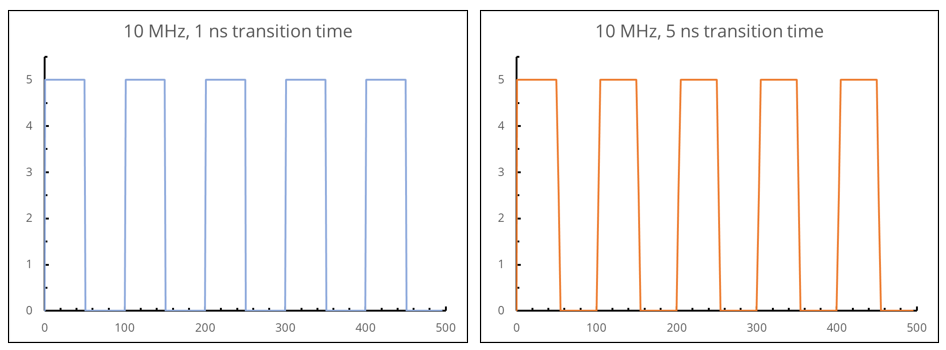
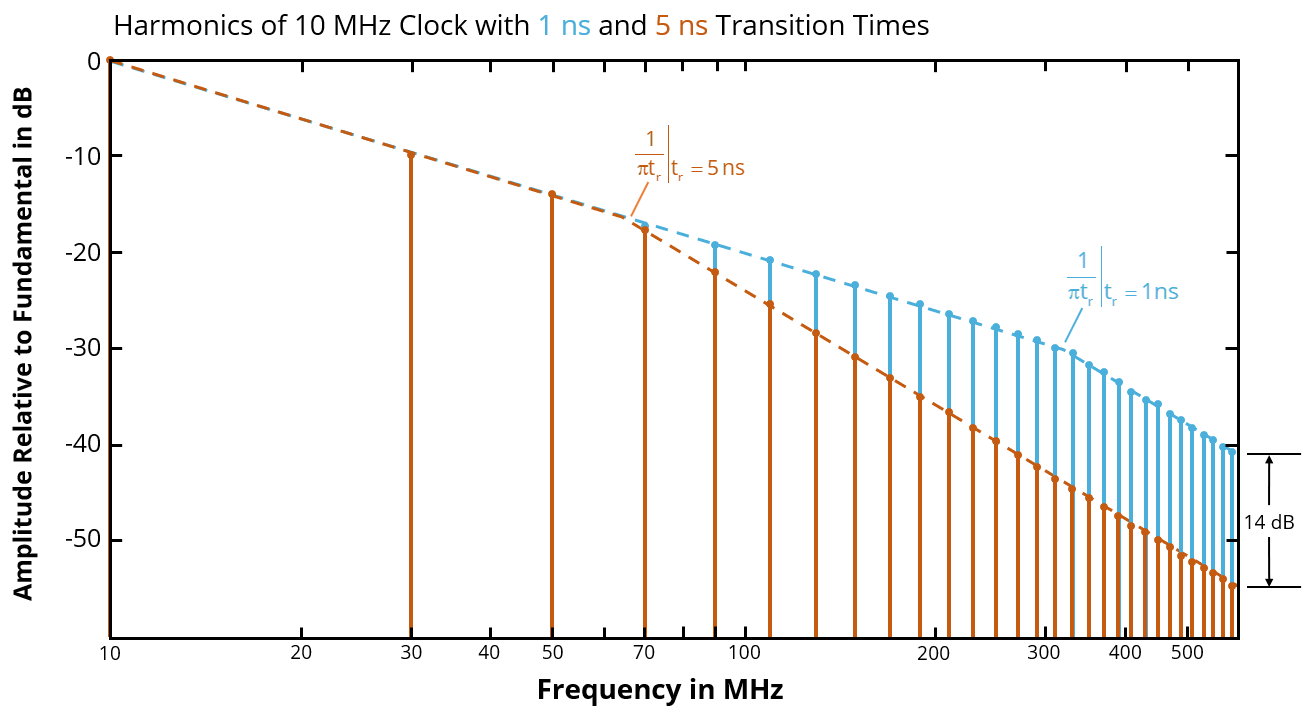
Slowing the transition time of a 10 MHz trapezoidal waveform from 1 ns to 5 ns reduces the maximum amplitude of harmonics above 320 MHz by
- 0 dB
- 5 dB
- 7 dB
- 14 dB
Answer
The best answer is “d.” Harmonics fall off at a rate of 20 dB/decade until they reach the transition time cut-off frequency, 1/πtr. For a 1-ns transition time, this cutoff occurs at 318 MHz. For a 5-ns transition time, the cutoff occurs at 64 MHz. The maximum amplitude of harmonics above the highest cut-off frequency is reduced by the ratio of the transition times. In this example, that's a factor of 5 (or 14 dB).
Most digital signal sources will transition in less than 1 ns by default. It is often important to control the transition times of these signals to reduce the amount of power in the upper harmonics. As indicated in the time-domain plots above, transition times on the order of 5% of the clock period produce good looking digital waveforms, while minimizing crosstalk and radiated emissions problems associated with transitions that are too fast.
Note that the amplitude of every harmonic above the cut-off frequency doesn't drop exactly 14 dB. It is the envelope (the maximum amplitude) that drops 14 dB. Changes to the transition time change the location of nulls in the harmonics. This will increase the amplitude of some upper harmonics and reduce the amplitude of others. However, all of the harmonics have amplitudes that are at or below the envelope.
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
