EMC Question of the Week: October 17, 2022

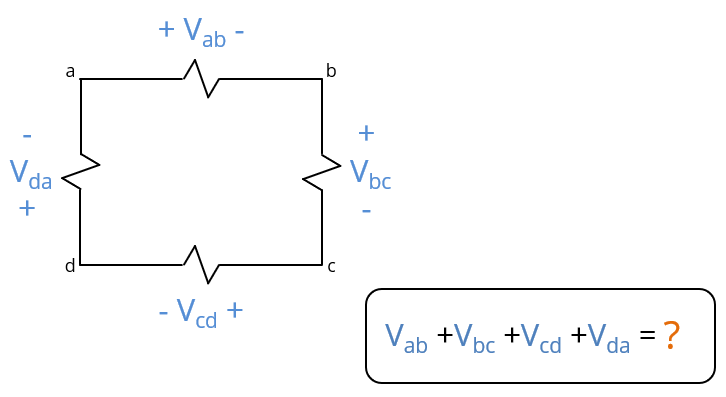
schematic showing four resistors connected in a loop

Faraday's Law says that the sum of the voltages around a closed loop is always equal to 

  1. zero
  2. loop current times resistance
  3. loop current times inductance
  4. ∂/∂t [magnetic flux passing through loop]

Answer

The correct answer is “d.” The sum of the voltages in a loop is always equal to the time rate of change of the magnetic flux passing through the loop. Or stated another way,

∮ E → ⋅ d ℓ → = − ∂ ∂ t   ∫ S B → ⋅ d s → .

Faraday's Law is one of Maxwell's Equations. Like the other Maxwell's Equations, it always holds. For DC circuits, Faraday's Law guarantees that the sum of voltages around any circuit loop (or mesh in a SPICE model) is zero. This is essentially a statement of Kirchoff's voltage law.

However, for AC circuits, Faraday's law essentially guarantees that the sum of the voltages in any circuit loop is not zero if there is current flowing in any portion of the loop. That's because a time-varying current will induce a time-varying flux that couples the loop.

Nevertheless, we generally rely on Kirchoff's voltage law to do circuit analysis. It works well enough as long as the voltages induced by the loop currents (and the ambient fields) produce voltages that are negligible compared to the signal voltages in the circuit. At higher frequencies, where the flux produced by the loop currents induces non-negligible voltages in the circuit, circuit analysis based on Kirchoff's voltage law can still be applied by including lumped inductors in the model to account for the parasitic loop inductances and/or mutual inductances.

Note that Faraday's Law not only applies to circuit loops, but to any loop defined anywhere in space. And while the voltage between two points in space is not uniquely defined, the voltage along a given path between two points in space is well-defined and is always,

V a b = ∫ a b E → ⋅ d ℓ. →

Have a comment or question regarding this solution? We'd like to hear from you. Email us at This email address is being protected from spambots. You need JavaScript enabled to view it..