EMC Question of the Week: September 26, 2022

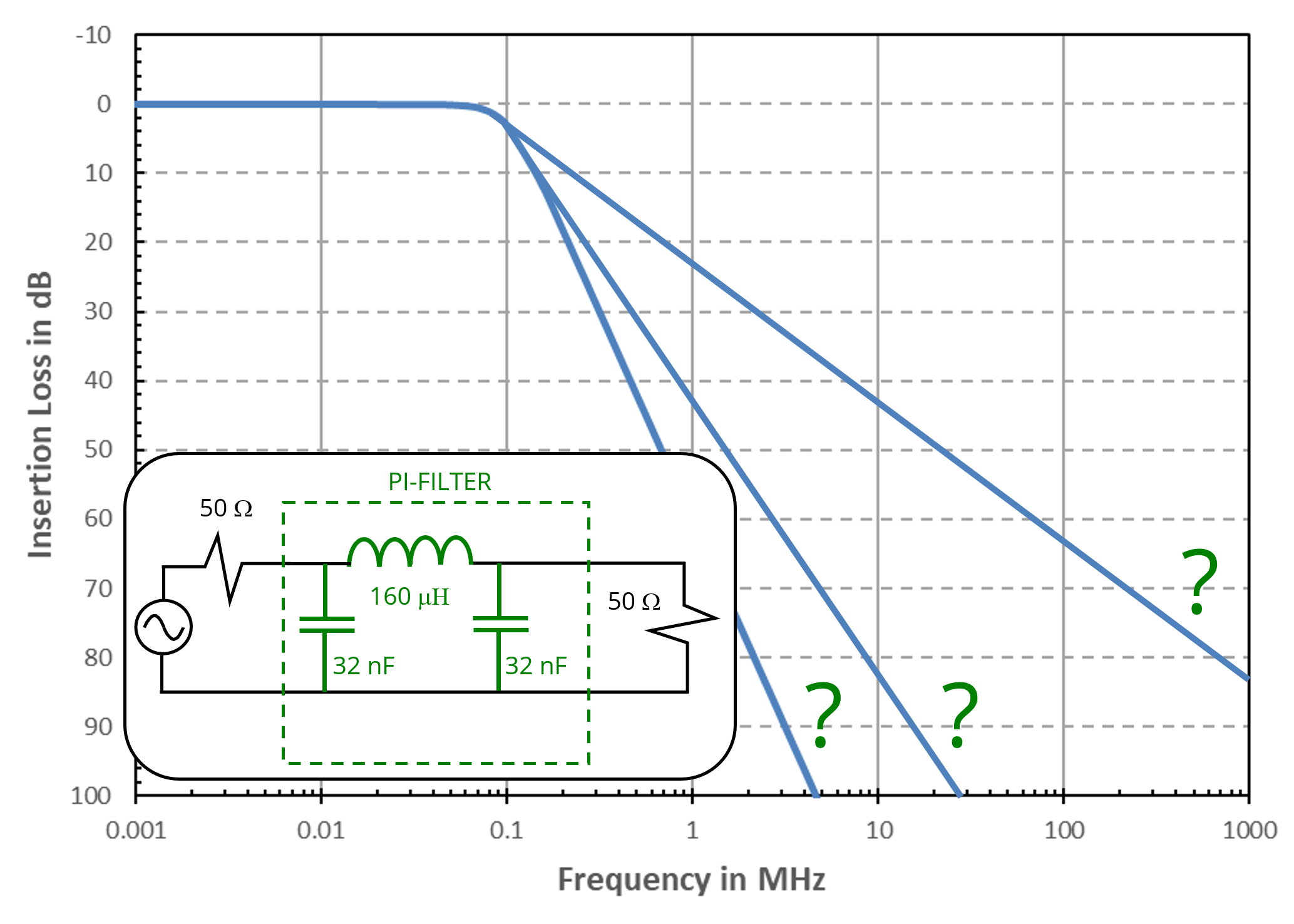
Which insertion loss plot is correct for this pi-filter?

Above the cut-off frequency, the insertion loss of an ideal low-pass pi-filter increases at a rate of 

  1. 20 dB/decade
  2. 40 dB/decade
  3. 60 dB/decade
  4. 6 dB/octave

Answer

The best answer is “c.” A pi-filter is a 3rd-order filter with an insertion loss that increases at a rate of 60 dB/decade when it is properly matched to the source and load resistances. 60 dB/decade is another way of expressing an increase proportional to the frequency cubed. 

First-order low-pass filters (series inductor or shunt capacitor) have an insertion loss that is proportional to frequency. Matched 2nd-order filters have an insertion loss proportional to the frequency squared. 20 dB/decade and 6 dB/octave are both ways of expressing an increase (or decrease) directly proportional to the frequency. 40 dB/decade is a rate proportional to the frequency squared.  

Pi-filters are often used on power inputs where the source and load impedances depend on the application and may not be well-defined. In these situations, the filter may have two different cut-off frequencies, and it may even exhibit a negative insertion loss near one or both of those cut-off frequencies. It's important to understand the range of possible source and load impedances (both resistance and reactance) when designing any filter.

Another problem with pi-filters is that parasitic coupling can result in an actual insertion loss that is much different from the calculated value. The higher the order of the filter, the more difficult it becomes to account for the parasitic coupling. To achieve the best possible performance over the widest possible bandwidth, most EMC filters are 1st-order filters, while 4th- and higher-order filters are rarely utilized. 

Note: Insertion loss is typically plotted with the vertical axis inverted (i.e., higher values at lower positions). That is why we refer to the insertion loss as "increasing" at a rate of 60 dB/decade even though the slope of the curve is down.

Have a comment or question regarding this solution? We'd like to hear from you. Email us at This email address is being protected from spambots. You need JavaScript enabled to view it..