EMC Question of the Week: May 30, 2022
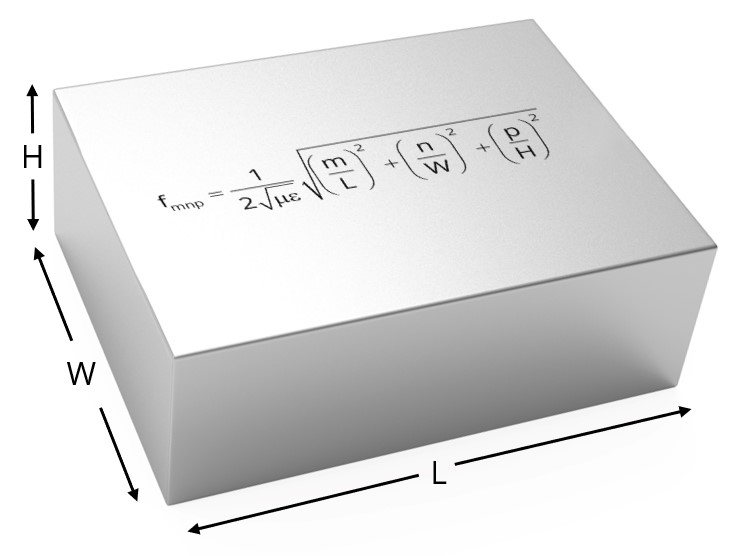
For a rectangular metal enclosure whose length is greater than its width, and whose width is greater than its height, the lowest resonant frequency is a function of its
- length only
- length and width only
- length, width and height
- height only
Answer
The best answer is “b.” The resonance frequencies of a dielectric-filled rectangular metal enclosure are given by the expression,
where L, W and H are the dimensions of the enclosure; μ and ε are the permeability and permittivity of the dielectric that fills the cavity; and m, n and p are non-negative integers (at least two of them non-zero). When L>W>H, the lowest resonant frequency is f110. The two longest dimensions determine the lowest resonant frequency.
For cavity resonances between planes in a rectangular circuit board, the lowest resonant frequency is the TM001 mode. This is because the edges are not shorted and can support a non-zero tangential electric field. The lowest resonant frequency supported by planes in a rectangular circuit board is therefore a function of the longest dimension only. It occurs when the longest plane dimension is approximately one half-wavelength in the cavity dielectric.
The lower resonant frequencies of rectangular enclosures and circuit boards can be calculated using a cavity resonance calculator.
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
