EMC Question of the Week: January 31, 2022
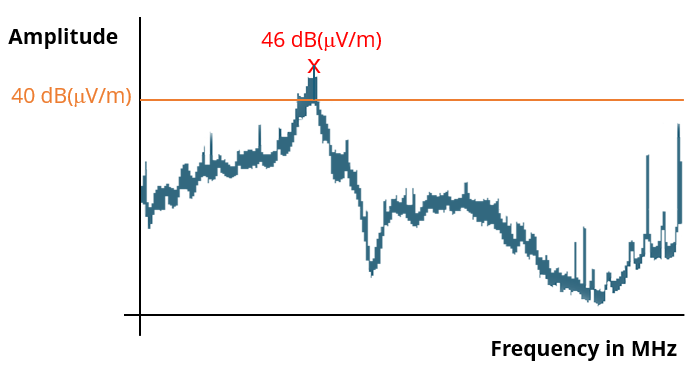
The quasi-peak amplitude in a radiated emissions measurement is 46 dB(μV/m). The quasi-peak limit at that frequency is 40 dB(μV/m). The measured value is over the limit by
- 6 dB(μV/m)
- 12 dB(μV/m)
- 20 dB(μV/m)
- 40 dB(μV/m)
Answer
The correct answer is “d.” Although, EMC engineers would rarely describe it this way. The measured amplitude is 46 dB(μV/m), which is 200 μV/m. The limit is 40 dB(μV/m), which is 100 μV/m. Therefore, the measurement is over the limit by 200 μV/m - 100 μV/m = 100 μV/m, which is 40 dB(μV/m).
Electrical engineers often compare the amplitudes of two signals by subtracting their amplitudes. For example, "the 25-volt rating of that capacitor is only 1 volt higher than the 24-volt power bus it's connected to." But for large differences, it's much more common to express the relative amplitudes of two signals as a ratio. For example, the 25-volt rating of that capacitor is 5 times the peak voltage in that 5-volt signal.
In the example cited in this problem, an EMC engineer is unlikely to express the relationship between the measured signal and the limit as a field strength. It is clearer and more concise to express the ratio of the two values. In this case, 46 dB(μV/m) - 40 dB(μV/m) = 6 dB. In other words, the measured field has an amplitude that is twice as high as (or 6 dB over) the limit.
Note that it is incorrect to say that the measured field is 6 dB(μV/m) above the limit. 6 dB(μV/m) is 2 μV/m. 6 dB(μV/m) above the limit would be 102 μV/m, which is only 0.17 dB above the limit.
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
