EMC Question of the Week: March 15, 2021

For a pair of identical circuit board traces over a ground plane, the difference between differential-mode propagation and odd-mode propagation is

1. differential-mode is undefined
2. odd-mode is undefined
3. a factor of 2
4. there is no difference

Answer

The best answer is “d.” For identical traces, differential-mode propagation is the same as odd-mode propagation. In both cases, one trace is driven with a positive voltage and the other with an equal-magnitude negative voltage relative to the plane. Common-mode (or even-mode) propagation occurs when both traces are driven with the same voltage relative to the plane.

The terms differential-mode and common-mode are well-defined even if the signal carrying conductors have different geometries. The terms odd-mode and even-mode are only applied when the two signal carrying conductors are identical (or have the same impedance to ground).

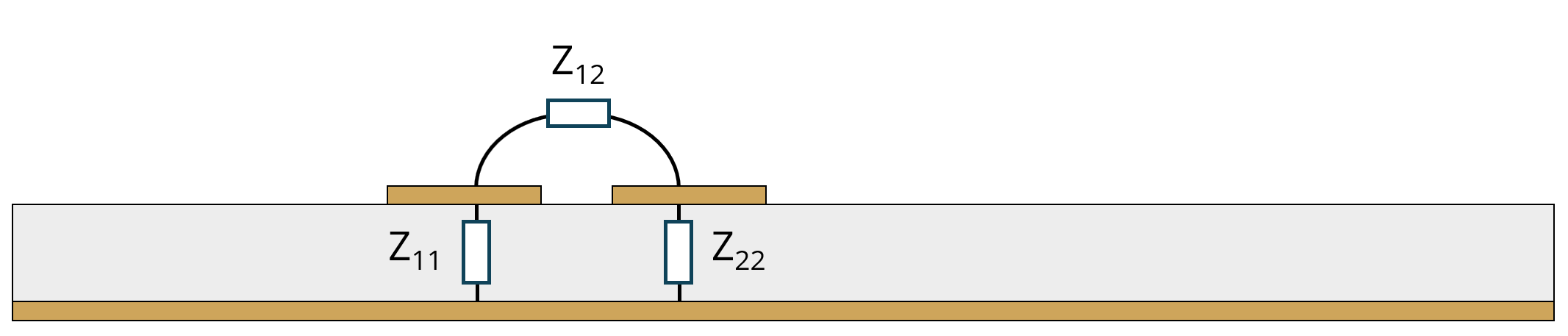
Differential-mode and common-mode are orthogonal propagation modes. In other words, the voltages and currents associated with one mode are independent of the voltages and currents associated with the other mode. The characteristic impedance of the differential-mode propagation is equal to $Z_{DM}=Z_{12}‖\left(Z_{11}+Z_{22}\right)$, where Z₁₁ and  Z₂₂ are the trace-to-ground impedances and Z₁₂ is the trace-to-trace impedance as indicated in the figure. The characteristic impedance of the common-mode propagation is $Z_{CM}=Z_{11}‖Z_{22}$.

Odd-mode and even-mode impedances are defined in terms of a single trace assuming the trace pair is identical. The odd-mode impedance is always one-half the differential-mode impedance (Z_ODD1 = Z_ODD2 = Z_DM/2). The even-mode impedance is always twice the common-mode impedance (Z_EVEN1 = Z_EVEN2 = 2*Z_CM).

Have a comment or question regarding this solution? We'd like to hear from you. Email us at This email address is being protected from spambots. You need JavaScript enabled to view it..