EMC Question of the Week: September 21, 2020
The input signal of a two-port linear network is sinusoidal with an rms amplitude of 1 volt and a frequency of 100 MHz. What MUST be true about the output signal?
- The amplitude must be 1 volt or less.
- It must be sinusoidal.
- It can only have components at DC and harmonics of 100 MHz.
- It must have the same power as the input signal.
Answer
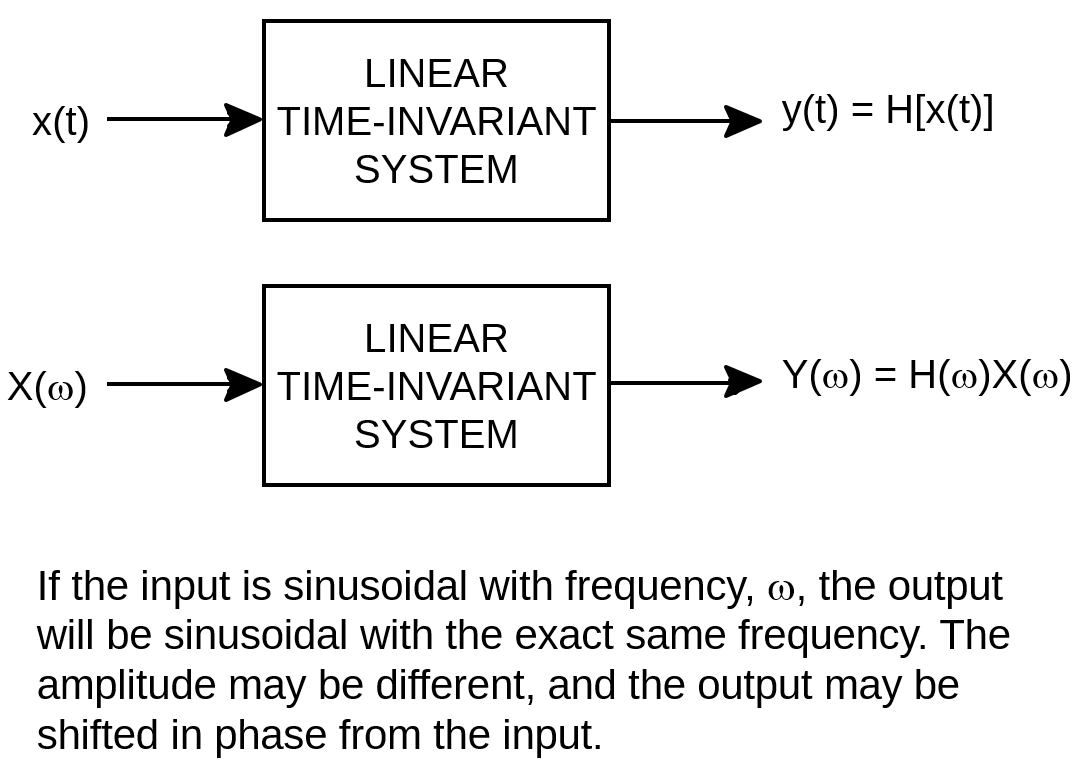
The correct answer is "b". Linear system theory is the mathematical workhorse used in virtually every field of engineering. And while it can be argued that all real, physical systems are non-linear. Engineers like to define ranges of linear (or nearly linear) operation, which allows them to model fairly complex systems using relatively simple math.
A key feature of linear systems is that a sinusoidal input will always produce a sinusoidal output at exactly the same frequency. Only the magnitude and phase can be changed. This allows engineers to represent the signal at a given frequency at any point within the system by a single complex number (magnitude and phase). Linear systems can be fully described by sets of complex functions of frequency such as transfer functions, Z-parameters, S-parameters and others.
If the input is sinusoidal, the output cannot have a DC component or components at any harmonics other than the fundamental frequency. In fact, the presence of output frequencies other than the input frequency is a clear indication that something non-linear is occurring.
Generally, there is no requirement that the output have an amplitude less than the input. Although, power in the output of a passive linear system cannot be greater than the input power.
Note: Another key feature of linear systems is superposition (i.e. if the input can be expressed as the sum of 2 or more signals, the output is the sum of the outputs that would have resulted from each of those input signals individually). Therefore, if we can represent input signals as a sum of sinusoids, the output will be the sum of the outputs for each sinusoidal component.
Have a comment or question regarding this solution? We'd like to hear from you. Email us at
