Electromagnetic Shielding Effectiveness Calculator

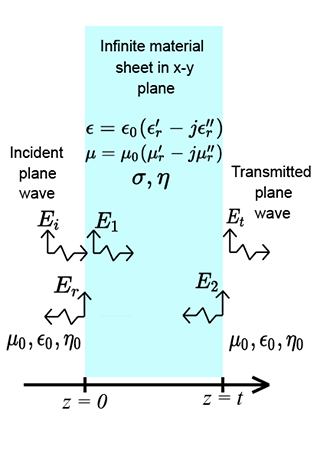
Basic definitions:

Permittivity	Permeability	Propagation constant	Skin depth	Free space intrinsic impedance	Material intrinsic impedance
$\epsilon=\epsilon_0(\epsilon_r' - j\epsilon_r'')$	$\mu = \mu_0 (\mu_r' - j\mu_r'')$	$\gamma=\sqrt{j\omega\mu(\sigma+j\omega\epsilon)}$	$\delta = \frac{1}{\Re\left( \gamma \right)}$	$\eta_o = \sqrt{\frac{\mu_0}{\epsilon_0}}$	$\eta = \sqrt{\frac{j \omega \mu}{\sigma + j \omega \epsilon}}$

Transmission coefficient into material	Transmission coefficient out of material	Reflection coefficient into material	Reflection coefficient out of material
$T_\eta = \frac{2 \eta}{\eta + \eta_0}$	$T_{\eta_0} = \frac{2 \eta_0}{\eta + \eta_0}$	$\Gamma_\eta = \frac{\eta-\eta_0}{\eta + \eta_0}$	$\Gamma_{\eta_0} = \frac{\eta_0 - \eta}{\eta + \eta_0}$

Equations for transmitted, reflected and absorbed power normalized to the incident power:

Transmittance	Reflectance	Absorbance
$\hat{P}_T = \frac{P_T}{P_I} = \left| T_{\eta} T_{\eta_0} \frac{1}{1 - \Gamma_{\eta_0}^2 e^{-2 \gamma t}} e^{- \gamma t} \right|^2 $	$\hat{P}_R =\frac{P_R}{P_I} = \left| \Gamma_\eta + \frac{T_\eta T_{\eta_0} \Gamma_{\eta_0} e^{-2\gamma t}}{1-\Gamma_{\eta_0}^2 e^{-2\gamma t}} \right|^2$	$\hat{P}_A = 1 - \hat{P}_T - \hat{P}_R $

The Mismatch Decomposition breaks the overall shielding effectiveness value into reflective and absorptive components called the Mismatch Loss and Dissipation Loss as descibed in references [1]-[3].

Effective absorbance	Mismatch Loss	Dissipation Loss
$\hat{P}_{A,eff} = \frac{\hat{P}_A}{1-\hat{P}_R}$	$R_{eff} = -10 \log_{10} \left( 1-\hat{P}_R \right)$	$A_{eff} = -10 \log_{10} \left( 1 - \hat{P}_{A,eff} \right) $ $\,\,\,= -10 \log_{10} \left(\frac{\hat{P}_T}{1-\hat{P}_R} \right)$
Shielding effectiveness: $\text{SE} = R_{eff} + A_{eff}$

The Schelkunoff Decomposition breaks the overall shielding effectiveness value into three components: Reflection Loss (R), absorption loss (A) and a multiple reflections correction term (M), as described in references [4]-[6].

Reflection Loss	Multiple Reflections Correction	Absorption Loss
$R = 20 \log_{10} \left| \frac{1}{T_\eta T_{\eta_0}} \right| $	$M = 20 \log_{10} \left| 1 - \Gamma^2 e^{-2 \gamma t} \right| $	$A = 20 \log_{10} \left| e^{\gamma t} \right| $
Shielding effectiveness: $\text{SE} = -10\log_{10}\left( \hat{P}_T \right) = R + M + A$

An alternative method of describing the decomposition of shielding into absorptive and reflective components is by relative absorption loss and relative reflection loss as shown below:

Relative reflection loss	Relative absorption loss
$R_{rel} = 10 \log_{10}\left( \sqrt{\frac{1}{\hat{P}_T} \frac{\hat{P}_R}{\hat{P}_A}} \right) $ $\,\,\,= \text{SE}/2 + 10 \log_{10}\left( \hat{P}_R / \hat{P}_A \right) / 2$	$A_{rel} = 10 \log_{10}\left( \sqrt{\frac{1}{\hat{P}_T} \frac{\hat{P}_A}{\hat{P}_R}} \right)$ $\,\,\, = \text{SE}/2 - 10 \log_{10}\left( \hat{P}_R / \hat{P}_A \right) / 2$
Shielding effectiveness: $\text{SE}= R_{rel} + A_{rel}$

1. M. Lin and C. H. Chen, “Plane-Wave Shielding Characteristics of Anisotropic Laminated Composites,” IEEE Trans. Electromag. Compat., vol. 35, no. 1, pp. 21–27, 1993.
2. Y. K. Hong, C. Y. Lee, C. K. Jeong, D. E. Lee, K. Kim, and J. Joo, “Method and apparatus to measure electromagnetic interference shielding efficiency and its shielding characteristics in broadband frequency ranges,” Rev. Sci. Instrum., vol. 74, no. 2, p. 1098, 2003.
3. A. J. McDowell and T. H. Hubing, "Analysis and Comparison of Plane Wave Shielding Effectiveness Decompositions," IEEE Trans. Electromag. Compat., vol. 56, no. 6, pp. 1711-1714, Dec. 2014.
4. S. A. Schelkunoff, Electromagnetic Waves, Princeton, NJ: D. Van Nostrand, 1943.
5. R. B. Schulz, V. C. Plantz, and D. R. Brush, "Shielding theory and practice," IEEE Trans. Electromagn. Compat., vol. 30, no. 3, pp. 187–201, 1988.
6. C. R. Paul, Introduction to Electromagnetic Compatibility, John Wiley & Sons, Inc., 1992.

---

Notes on calculator usage:

• Parameters can be entered as numbers or as expressions in terms of frequency, defined as f, using the +,-,/,^ operators, and the following functions: sin, cos, tan, exp, log, log10, abs, acos, asin, atan. Also, the following constants are defined: pi, e, epsilon_0, mu_0, and eta_0.
• Zoom into plots by selecting box on the plot with the mouse.

These approximate equations are simplifications of the exact equations as in reference [1]. These equations assume the material is a good conductor with thickness much greater than a skin depth: \eta≪\eta₀ and \delta≪t.

Permeability	Skin depth	Free space intrinsic impedance	Material intrinsic impedance
$\mu=\mu_0 \mu_r$	$\delta ≈ \frac{1}{\sqrt{π f \mu_0 \mu_r \sigma}}$	$\eta_o = \sqrt{\mu_0/\epsilon_0}$	$\eta ≈ \sqrt{\frac{\omega \mu}{\sigma}} ∠ 45°$

Reflection loss	Absorption loss	Shielding effectiveness
$R_\text{dB} ≈ 20 \log_{10} \left| \frac{\eta_0}{4 \eta_s} \right| $	$A_{\text{dB}} = 20 \log_{10} \left| e^{t / \delta} \right| ≈ 8.7 t/\delta$	$\text{SE}_\text{dB} ≈ R_\text{dB} + A_\text{dB}$

1. C. R. Paul, Introduction to Electromagnetic Compatibility, John Wiley & Sons, Inc., 1992.

Notes on calculator usage:

• Parameters can be entered as numbers or as expressions in terms of frequency, defined as f, using the +,-,/,^ operators, and the following functions: sin, cos, tan, exp, log, log10, abs, acos, asin, atan. Also, the following constants are defined: pi, e, epsilon_0, mu_0, and eta_0.
• Zoom into plots by selecting box on the plot with the mouse.

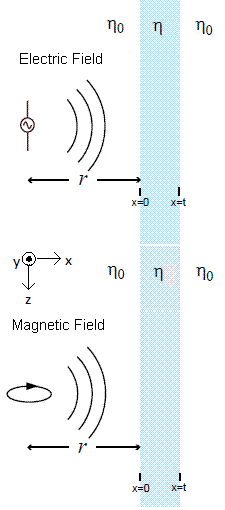
An approximation of near fielding shielding effectiveness can be made by using the plane wave shielding formulas in the exact tab (or simplifications of these formulas) with the wave impedance used in place of \eta₀ as in reference [1]. The wave impedance is defined as the ratio of the magnitudes of the transverse components of E and H at the wavefront. This approximation considers two z-directed elementary sources: a Hertzian electric dipole (an infinitesimal wire carrying current along the z-axis) and a magnetic dipole (an infinitesimal wire loop carrying current around the z-axis). For $\eta_0 = \sqrt{\mu_0/\epsilon_0}$, $\beta_0 = \omega \sqrt{\mu_0 \epsilon_0}$, and $r$ being the distance from the dipole to the wavefront, the wave impedances of these sources are given by:

Electric dipole wave impedance	Magnetic dipole wave impedance
$Z_{W_E} = \frac{E_θ}{H_ϕ} = \eta_{0} \frac{\frac{j}{\beta_{0} r} + \frac{1}{\left(\beta_{0} r\right)^{2}} - \frac{j}{\left(\beta_{0} r\right)^{3}}}{\frac{j}{\beta_{0} r} + \frac{1}{\left(\beta_{0} r\right)^{2}}}$	$Z_{W_M} = \frac{E_ϕ}{H_θ} = - \frac{\eta_{0}^2}{Z_{W_E}}$

Then near field shielding effectiveness approximations can be made by using these wave impedances with the plane wave shielding formulas. Note that this method of calculating near field shielding is approximate because the waves in the near field have a reactive wave impedance and also have radial field components. Additionally, this analysis neglects differences in the wave impedance on either side of the shield. However, also note that the wave impedance expressions both approach $\eta_0$ as $r \rightarrow \infty$, so that the calculations with this method will approach the exact plane wave calculations for large $r$.

1. C. R. Paul, Introduction to Electromagnetic Compatibility, John Wiley & Sons, Inc., 1992.

Notes on calculator usage:

• Parameters can be entered as numbers or as expressions in terms of frequency, defined as f, using the +,-,/,^ operators, and the following functions: sin, cos, tan, exp, log, log10, abs, acos, asin, atan. Also, the following constants are defined: pi, e, epsilon_0, mu_0, and eta_0.
• Zoom into plots by selecting box on the plot with the mouse.