Common Impedance Coupling

If you've ever noticed the lights flicker when a large home appliance kicks on, you have some experience with common impedance coupling. Common impedance coupling (also called conducted coupling) may occur anytime a source circuit and a victim circuit share part of their respective current paths.

Consider the two simple circuits shown in Figure 1. Each circuit has its own source, signal wire and load, but they both share a wire for the signal return current. If the shared wire had zero impedance, the voltage across each circuit's load resistor would depend only on that circuit's source voltage. However, a small amount of impedance in the shared wire causes a voltage to appear across R_L2 when there is a signal in Circuit 1 and vice versa.

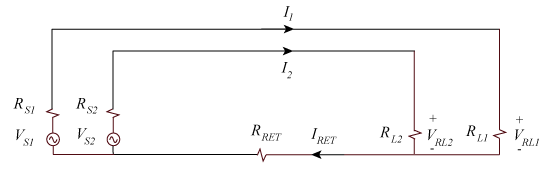
Two circuits sharing a common signal return wire

Figure 1: Two circuits sharing a common signal return.

This phenomenon is called crosstalk. Crosstalk is a term commonly used to describe the unintentional electromagnetic coupling between two circuits or systems in close proximity. Although there is no accepted standard for quantifying crosstalk, it is often expressed as a ratio of the coupled voltage in the victim circuit to the signal voltage in the source circuit. In this case, we’ll calculate the crosstalk as,

$crosstalk in dB = 20 \log | \frac{coupled voltage appearing at receiver in Circuit 2}{signal voltage in Circuit 1} |$ (1)

or,

${Xtalk}_{21} = 20 \log {| \frac{V_{R L 2}}{V_{R L 1}} |}_{w h e n V_{S2} = 0}$ . (2)

To calculate the crosstalk in Circuit 2 due to the signals in Circuit 1, we set V_S2 = 0 and determine the ratio V_RL2/V_RL1. Applying Kirchhoff's voltage law (KVL) to the Circuit 2 current loop, we have

$V_{S 2} + I_{2} R_{S 2} + I_{2} R_{L 2} + (I_{1} + I_{2}) R_{R E T} = 0$ (3)

Setting V_S2 = 0, we can rewrite Equation (3) to express I₂ in terms of I₁,

$I_{2} = \frac{- R_{R E T}}{R_{S 2} + R_{L 2} + R_{R E T}} I_{1}$ . (4)

Noting that I₁ = V_RL1/R_L1 and I₂ = V_RL2/R_L2, we can express Equation 4 in terms of the voltages across the load resistances,

$\frac{V_{R L 2}}{R_{L 2}} = \frac{- R_{R E T}}{R_{S 2} + R_{L 2} + R_{R E T}} \frac{V_{R L 1}}{R_{L 1}}$ . (5)

The crosstalk can now be expressed as,

$20 \log | \frac{V_{R L 2}}{V_{R L 1}} | = 20 \log | \frac{R_{R E T}}{R_{S 2} + R_{L 2} + R_{R E T}} \frac{R_{L 2}}{R_{L 1}} |$ . (6)

Example 4-1: Calculating the crosstalk between two 50-ohm circuits

For the circuit in Figure 1, let R_S1 = R_L1 = R_S2 = R_L2 = 50 ohms and assume the resistance of the signal return wire is 100 milliohms. The crosstalk is then,

$X t a l k_{21} = 20 \log [\frac{0.1}{50 + 50 + 0.1} (\frac{50}{50})] = - 60 dB$ . (7)

In other words, a signal voltage of 5 volts in Circuit 1 creates 5 mV of noise in Circuit 2.

Generally, for practical common impedance coupling situations, the impedance of the common return path will be much less than the load impedances of either circuit. Otherwise, the return path would severely attenuate the signals. In most cases, it is much quicker to estimate the voltage dropped across the signal return path as,

$V_{R E T} = I_{s i g n a l} R_{R E T}$ . (8)

In the case above, I_signal was I₁, the intentional current. Once we have estimated V_RET, we can use KVL to determine what fraction of this voltage appears across the victim circuit's load resistance. In this case,

$\begin{array}{l} V_{R L 2} \approx \frac{R_{L 2}}{R_{L 2} + R_{S 2}} V_{R E T} \\ \approx \frac{R_{L 2}}{R_{L 2} + R_{S 2}} R_{R E T} I_{1} \\ \approx \frac{R_{L 2}}{R_{L 2} + R_{S 2}} R_{R E T} \frac{V_{R L 1}}{R_{L 1}} \end{array}$ (9)

and the crosstalk is,

$X t a l k_{21} \approx 20 \log [\frac{R_{R E T}}{R_{L 2} + R_{S 2}} (\frac{R_{L 2}}{R_{L 1}})]$ . (10)

This approach generally yields very good estimates of the crosstalk and is much simpler to apply to complex configurations with many possible signal return paths.

Example 4-2: Common Impedance Coupling in a Ribbon Cable

The 20-cm, 9-wire ribbon cable illustrated in Figure 2 carries an 8-bit data bus (8 data wires and 1 return wire). The resistance per unit length of each wire in the cable is 1.1 ohms per meter at 2.0 MHz. If each of the data lines is driven by a 10-ohm source and terminated with a 50-ohm resistance to the common return wire, calculate the crosstalk between any two data lines that is due to common impedance coupling at 2.0 MHz.

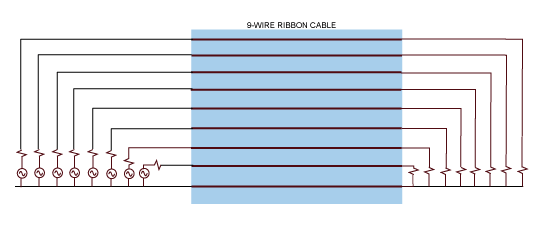
An 8-bit data bus on a 9-wire ribbon cable

Figure 2: An 8-bit data bus on a 9-wire ribbon cable

Due to the symmetry of this problem, we can start by turning any one of the sources on and the others off. In this case, the current in the source circuit will be,

$I_{1} = \frac{V_{R L 1}}{R_{L 1}}$ . (11)

After flowing through the load resistor, R_L1, the current can return to the source through the ribbon cable resistance or through the other 7 load and source resistances. The resistance of the return wire is,

$R_{w i r e} = 0.2 meters \times 1.1 Ω/m = 0.22 Ω$ . (12)

The resistance of the path through the other 7 source and load resistances in parallel is,

$R_{2 - 7} = \frac{R_{S} + R_{L} + R_{w i r e}}{7} = \frac{10 + 50 + 0.22}{7} = 8.6 Ω$ . (13)

Therefore, nearly all (98%) of the source current will return through the return conductor in the ribbon cable. The voltage dropped across the return conductor will then be,

$V_{R E T} = I_{1} R_{w i r e}$ . (14)

By voltage division, the voltage appearing across any of the other load resistors will be,

$V_{R L 2 - 7} \approx \frac{50}{10 + 50} V_{R E T} = 0.18 I_{1}$ (15)

and, therefore, the crosstalk can be expressed as,

$X t a l k = 20 \log [\frac{V_{R L 2 - 7}}{V_{R 1}}] = 20 \log [\frac{0.18 I_{1}}{50 I_{1}}] = - 49 dB$ . (16)

If the 9-wire ribbon cable is replaced with a 10-wire ribbon cable and the extra wire is used as an additional signal return, the resistance of the common return path is cut in half. This would reduce the crosstalk by a factor of 2 (i.e. 6 dB). In this case the total crosstalk would be -49 - 6 = -55 dB. Providing additional return conductors would reduce the crosstalk even more.

Note that the frequency of the signal never appeared in this crosstalk calculation. Common impedance coupling is independent of frequency except to the extent that the shared impedance is frequency dependent. At low frequencies (kHz and lower), the impedance of the wire would be independent of the frequency and so would the level of crosstalk. At high frequencies (MHz and higher), the resistance of the wire would be proportional to the square root of the frequency due to the skin effect. In this case, the crosstalk would also increase as the square root of the frequency; however common impedance coupling is not likely to be the dominant coupling mechanism at high frequencies.